No hemos encontrado resultados relativos a la búsqueda realizada.
Puedes volver a intentarlo de nuevo realizando una nueva búsqueda.
No hemos encontrado resultados relativos a la búsqueda realizada.
Puedes volver a intentarlo de nuevo realizado una nueva búsqueda.
Brazo Robótico con garra de apertura esférica en forma de iris para aplicaciones industriales
Por Carlos José García Mora

07 de Nov de 2022 · Gestión Integrada
El proyecto de investigación realizado como etapa final del Máster de Automatización Industrial, está centrado en el desarrollo y análisis de una garra robótica para aplicaciones industriales, tomando como referencia una patente de uno de los inventores españoles más influyentes en el campo de los sistemas desplegables: Emilio Pérez Piñero. La idea parte de extrapolar el concepto desarrollado en esta patente a una aplicación industrial, en donde varios segmentos o aletas esféricas se pliegan sincronizadamente para permitir la captura y transporte de objetos de diversa geometría.
Para conseguir tal objetivo, se comenzará con una profunda búsqueda de dispositivos tecnológicos con aplicaciones similares y luego, se expondrán diferentes casos de referencia, que servirán como inspiración para el diseño e implementación de la garra robótica. Una vez que, tanto su sistema mecánico como su dispositivo de activación han sido completamente definidos, se procederá no solo a estudiar su comportamiento en posición sino también a evaluar su cinemática en velocidad y aceleración. Tras el estudio completo de la garra robótica planteada, los siguientes apartados de este proyecto de investigación se focalizarán en el diseño de la electrónica de control con la respectiva selección de los componentes comerciales, la programación del software que será grabada en el microcontrolador y la propuesta de un presupuesto que englobe todas las etapas de fabricación y montaje. Por último, el proyecto se cierra con un abanico de potenciales campos de aplicación para esta innovación tecnológica seguido de las correspondientes conclusiones y listado de referencias.
¿Te resulta interesante?
¡Guarda este contenido completo en PDF!
Descarga gratis este contenido y consúltalo cuando lo necesites
1. INTRODUCCIÓN
El avance de la robótica a lo largo de los últimos años ha sido exponencial gracias al empleo de las nuevas herramientas de simulación numérica y de diseño asistido por ordenador (Babaee et al., 2020) (Escrig & Valcarcel, 1993). Estas mejoras han permitido incluso emular el comportamiento biológico de algunos animales marinos en lo que se refiere a nuevos manipuladores para desplazar objetos con cualquier geometría (Truby et al., 2019) (Chen & Feng, 2012) (Jin et al., 2020) (Figura 1).

Figura 1: Garra que emula el comportamiento biológico de unos tentáculos por Ryan L. Truby, Robert K. Katzschmann, Jennifer A. Lewis y Daniela Rus.
Desde un punto de vista muy genérico, un brazo robótico se puede subdividir en dos partes (Fomin et al., 2017) (García-Mora & Sánchez-Sánchez, 2020):
- La cadena de eslabones: Posibilitan el posicionado de la garra o manipulador en la ubicación deseada a través del trabajo conjunto de cada uno de los motores ubicados en sus articulaciones
- La garra o manipulador: Se ubica en el extremo final de la cadena de eslabones y permite coger, desplazar y soltar objetos
Este PFM se centra especialmente en el desarrollo de una garra o manipulador basado en el uso de segmentos esféricos para conseguir una apertura en forma de iris.
La idea de este nuevo manipulador tiene su origen en un artículo científico escrito por los investigadores de Harvard: Zhi Ern Teoh, Brennan T. Phillips, Kaitlyn P. Becker, Griffin Whittredge, James C. Weaver, Chuck Hoberman, David F. Gruber y Robert J. Wood (Teoh et al., 2018). Estos autores proponen una garra formada por una serie de eslabones constituyendo una cadena cinemática con una sola entrada de actuación (Chen et al., 2005).
Para ello, parten de un poliedro dodecaédrico el cual abate cada una de sus caras hasta quedar todas ellas contenidas en un solo plano. La sincronización de cada uno de sus movimientos se obtiene mediante un mecanismo que está conectado a cada una de las superficies (Escrig et al., 1996) (Cai et al., 2014) (Figura 2).
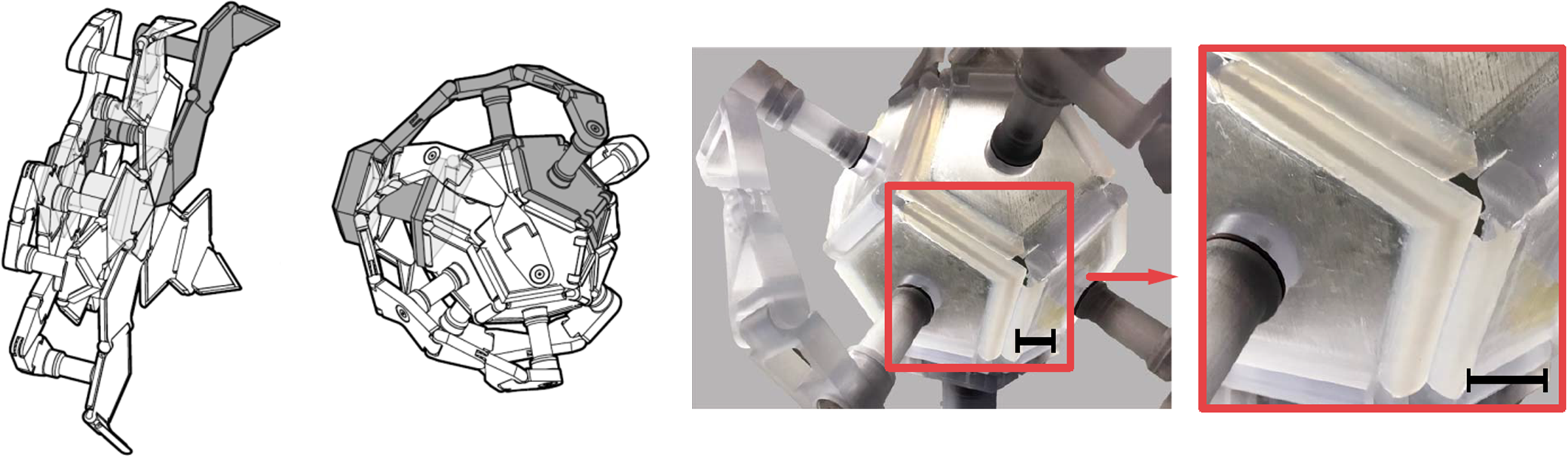
Figura 2: Garra con forma de poliedro dodecaédrico desarrollada por investigadores de Harvard.
El principal objetivo de este Proyecto Final de Master (PFM) consiste en proponer una garra que, teniendo las mismas prestaciones del manipulador diseñado por los investigadores de Harvard, resuelva algunas de sus desventajas como es la gran diferencia entre el área ocupada en posición abierta y el volumen atrapado en posición cerrada o la baja sensibilidad en la rotación de su activación. Para ello, se utilizará una tecnología ya desarrollada y patentada por uno de los inventores más importantes en el campo de las estructuras desplegables: Emilio Pérez Piñero (Pérez-Almagro, 2017) Básicamente, su invención consistió en extrapolar el dispositivo de diafragma plano de una cámara fotográfica a una superficie esférica resolviendo los consecuentes problemas tecnológicos que se podían plantear (Figura 3).
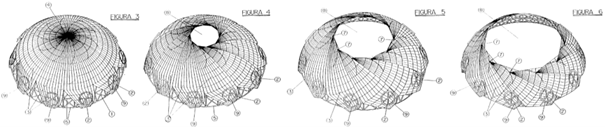
Figura 3: Imágenes de la patente registrada por Emilio Pérez Piñero (cúpula reticular practicable de directriz esférica).
2. ANTECENTES
2.1. Tipos de robots
2.1.1. Androides o zoomórficos
Se entiende por robot zoomórfico aquel robot que imita el comportamiento de los seres vivos a través de su propia locomoción. Dentro de los robots zoomórficos nos podemos encontrar con dos grupos: los no caminantes y los caminantes (Figura 4).

Figura 4: (izquierda) Robot zoomórfico no caminante – OmniTread snakebot por la Universidad de Michigan ; (derecha) Robot zoomórfico caminante - Boston Dynamics.
2.1.2. Móviles
Los robots móviles son aquellos que se desplazan mediante el uso de apoyos, orugas o ruedas teniendo como referencia la información obtenida a través de un conjunto de sensores (Figura 5).

Figura 5: (izquierda) Robot para cadena de suministros - Mobile Industrial Robots (MIR) ; (centro) Robot para exploración submarina - LarvaBot por la Universidad Tecnología de Queensland; (derecha) Robot de limpieza - iRobot Roomba i7.
2.1.3. Médicos
Uno de los primeros robots médicos de campo desarrollados data de 1980 y tenía como objetivo ser utilizado de apoyo en las intervenciones quirúrgicas, mediante el uso de varios brazos robóticos. Asimismo, su nula capacidad para transmitir patógenos y gérmenes los hacen especialmente útiles en el caso de pacientes que tienen que tener el mínimo contacto con el mundo exterior (Figura 6).
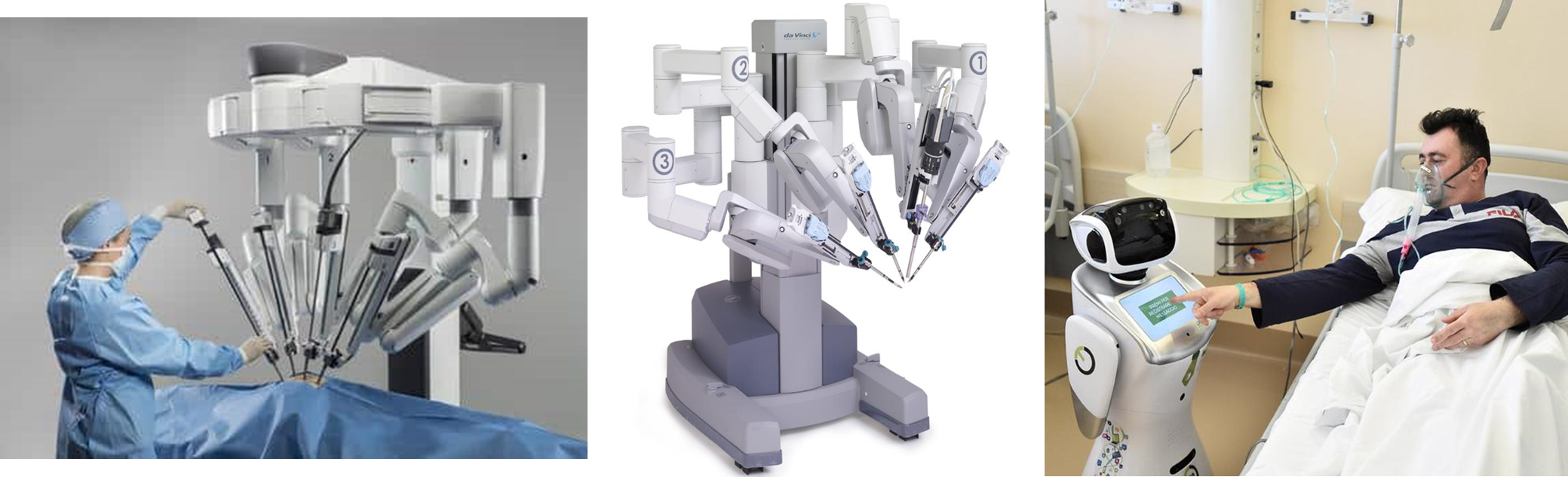
Figura 6: (izquierda y centro) Robot médico utilizados tanto para intervenciones quirúrgicas - Robot Da Vinci ; (derecha) Robot médico utilizado para cuidado de pacientes - Tommy, the robot nurse (Circolo hospital).
1.1.4. Industriales
Los robots industriales son los más extendidos en cuanto a uso y aplicación en el sector de la robótica debido a la continua necesidad de automatizar tareas altamente repetitivas y a los altos retornos de inversión económica que se obtienen una vez que el robot ha sido implementado. Dentro de este amplio grupo nos podemos encontrar con diferentes configuraciones de robots: cartesianos, SCARA, 6 ejes, teleoperados y colaborativos (Figura 7).

Figura 7: De izquierda a derecha: robot industrial (VIEWEG), robot SCARA (VIEWEG), robot de 6 ejes (EPSON) y robot colaborativo (ABB).
2.2. Casos de referencia
2.2.1. Canadarm 2
El Canadarm 2 o “Mobile Servicing System” (MSS) es un equipamiento robótico de la Estación Espacial Internacional (ISS) desarrollado por MacDonald, Dettwiler and Associates. Sus funciones radican en el movimiento de equipos y suministros y el apoyo en las tareas realizadas por los astronautas en el exterior de la estación (Tabla 1) (Figura 8).

Tabla 1: Propiedades del Canadarm 2.

Figura 8: Canadarm 2 desde el exterior de la ISS y dispositivo de conexión en sus extremos (Latching End Effector).
2.2.2. Dextre
El Dextre o “Special Purpose Dexterous Manipulator” (SPDM) está formado por dos brazos operados a distancia y fabricado por la empresa MDA Space Missions. Junto con el Canadarm y el Canadarm 2, Dextre es el tercer brazo robótico desarrollado por Canadá para la ISS (Tabla 2) (Figura 9).

Tabla 2: Propiedades del Dextre.

Figura 9: Dextre desde el exterior de la ISS.
2.2.3. European Robotic Arm (ERA)
ERA es un brazo robótico que está acoplado al Segmento Orbital Ruso (ROS) de la ISS siendo el primer brazo robótico con capacidad para trabajar en la parte rusa de la estación. El promotor inicial de ERA fue la Agencia Espacial Europea, la cual subcontrató parte de los trabajos a numerosas empresas siendo Airbus Defence and Space Netherlands el contratista principal (Tabla 3) (Figura 10).
|
Predecesor |
Lanzamiento |
Altitud |
Peso |
Longitud |
|
Canadarm 2 |
Julio de 2021 |
400 km |
630 kg |
11.3 m |
|
Carga |
Articulaciones |
Velocidad |
Precisión |
Consumo |
|
3000kg |
7 |
0.1 m/s |
5 mm |
475 W |
Tabla 3: Propiedades del ERA.

Figura 10: Despliegue de ERA en tierra y puntos de conexión (End Effectors o EES).
2.2.4. Rotary Actuated Dodecahedron (RAD)
El Rotary Actuated Dodecahedron (RAD) es una garra robótica diseñada para la captura de animales marinos (Teoh et al., 2018). Dicho dispositivo se fundamenta en el uso de un dodecaedro como volumen de captura: en posición plegada la garra tiene la geometría de este poliedro y en su interior se encontrará el animal marino capturado mientras que en posición desplegada, la garra tendrá una geometría casi plana (Figura 11). La principal innovación de este instrumento reside en la sincronización y coordinación de las superficies de la garra durante el plegado y desplegado. Para ello, se recurre a una cadena cinemática de eslabones con articulaciones orientadas en diferentes direcciones.

Figura 11: Captura de un organismo marino utilizando el RAD.
3. DESARROLLO
3.1. Descripción del funcionamiento
La idea más básica en la que se basa la garra desarrollada es el concepto del dispositivo diafragmático de una cámara fotográfica (Akgün et al., 2010). Desde un punto de vista mecánico, este utensilio se puede modificar mediante la inclusión de una doble capa de aletas que mejore la transmisión de esfuerzos (Gantes et al., 1989) e incluso se permite su conversión desde la geometría circular estándar a una geometría arbitraria utilizando el modelo de aspas quebradas equivalente (Arnouts et al., 2018) (Arnouts et al., 2020) (Alegria et al., 2014) (Figura 12).
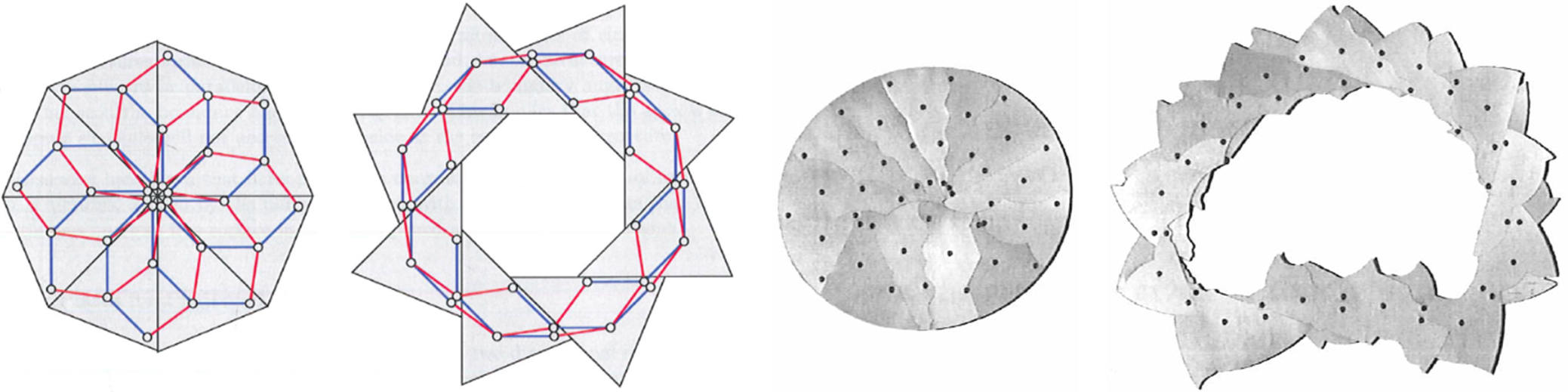
Figura 12: Diafragma de una cámara fotográfica con el respectivo modelo equivalente de barras quebradas y extrapolación del modelo a una geometría elíptica.
Sin embargo, este dispositivo tiene en todo momento una geometría plana, lo que limita bastante su utilidad. El inventor español, Emilio Pérez Piñero, resolvió este inconveniente hace 30 años extrapolando este sistema mecánico a una geometría esférica y extendiendo su uso al ámbito arquitectónico en forma de cúpulas retráctiles (Christoforou et al., 2015) (Kirsch, 1982) (Overvelde et al., 2017) (Figura 13).

Figura 13: Proceso de desplegado de una cúpula reticular de directriz esférica desarrollada y construida por Emilio Pérez Piñero.
A pesar del gran avance aportado por Emilio, este sistema tenía algunos problemas de colisiones geométricas (Gantes et al., 1991). Para resolver este conflicto, el inventor español colocó las aletas de forma alternada con un ligero incremento de su radio en uno de los grupos de las aletas. Esta estrategia de diseño permitía resolver las colisiones hasta un cierto número de subdivisiones en la esfera, siendo esta cantidad de 6 aletas para una rotación antihoraria y de 10 aletas para una rotación horaria (Liu et al., 2016). La solución a estas limitaciones de diseño apareció hace 15 años cuando el Dr. Frank Vadstrup publicó en su tesis doctoral una manera de solventar estas colisiones mediante la adaptación de la geometría de cada una de las aletas a la trayectoria de la aleta inmediatamente contigua. Dicho investigador construyó varios modelos a escala para demostrar el funcionamiento de su propuesta las cuales se pueden apreciar en la siguiente figura (Figura 14).

Figura 14: Sincronización de las aletas durante la apertura de la cúpula esférica por el Dr. Frank Vadstrup Jensen.
En este Proyecto Fin de Master lo que se ha hecho es extrapolar este concepto mecánico a una aplicación robótica y materializarla en un manipulador. En la siguiente figura se puede apreciar el proceso de desplegado del modelo final diseñado (Figura 15).
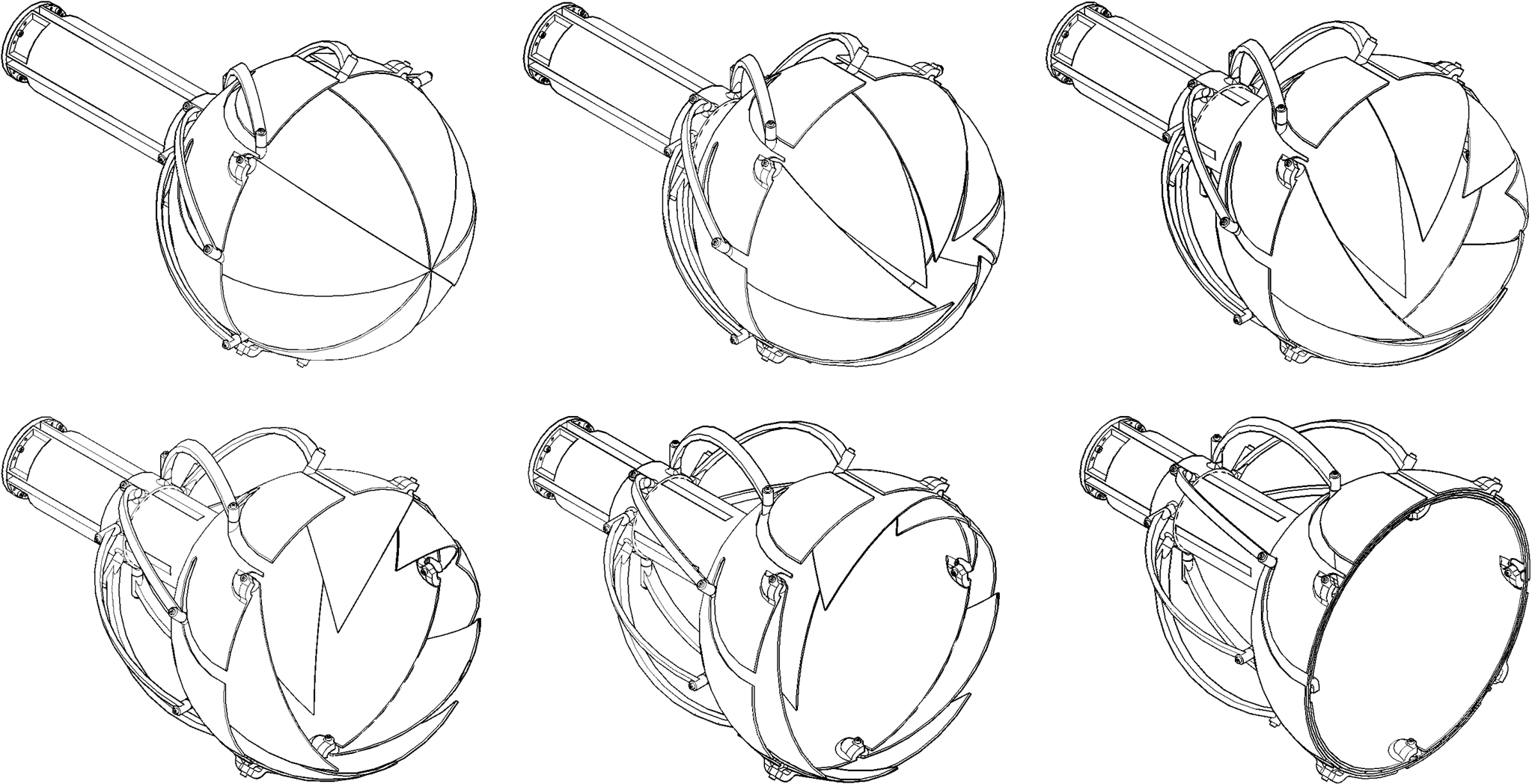
Figura 15: Proceso de desplegado de la garra desarrollada.
Las siguientes figuras son representaciones gráficas de los procesos de apertura y de cierre en vistas tanto frontales como en perspectiva (Figura 16) (Figura 17)

Figura 16: Vistas frontales del proceso de desplegado de la garra desarrollada.
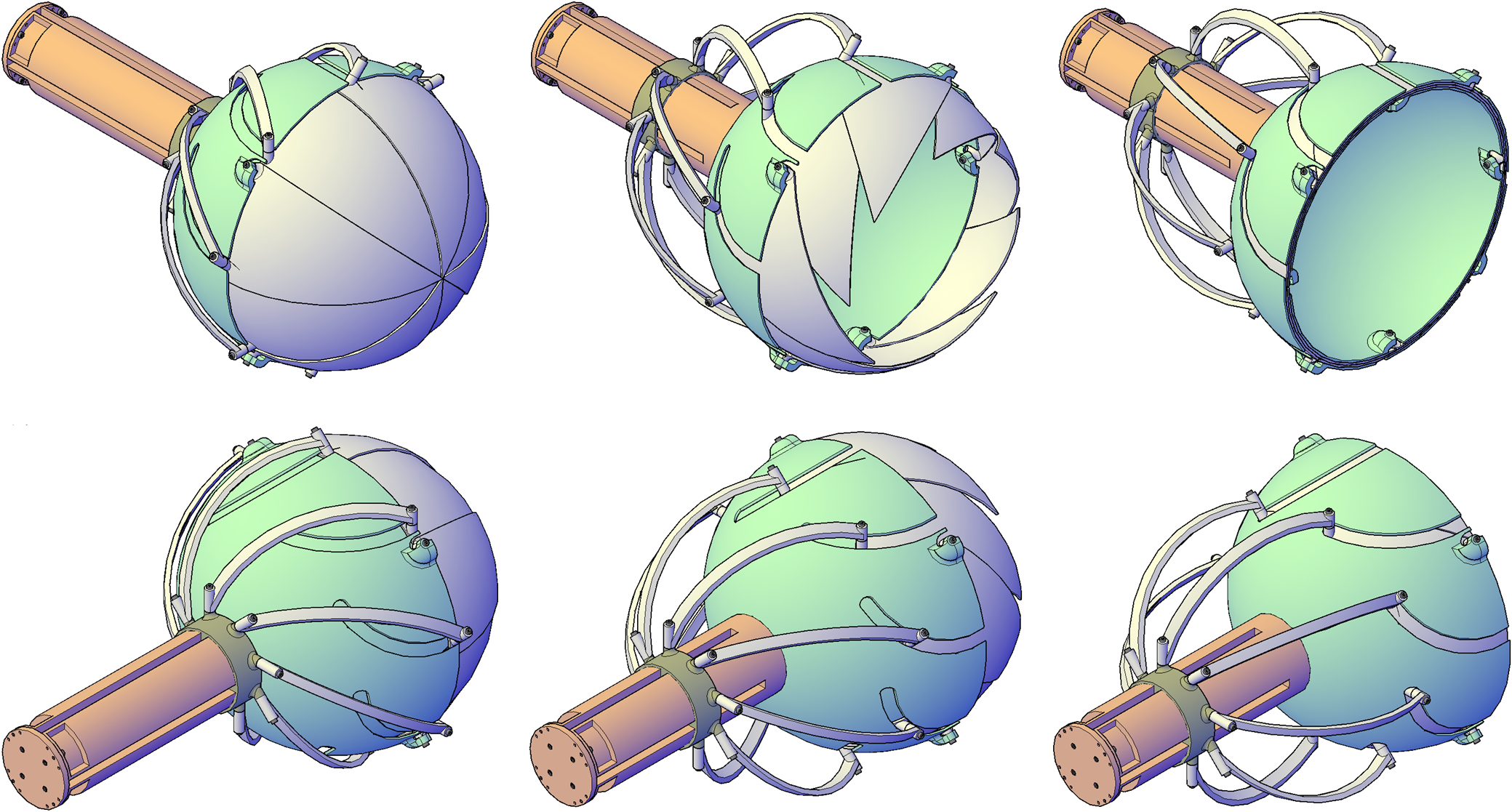
Figura 17: Perspectivas del proceso de desplegado de la garra desarrollada.
3.2. Identificación de los componentes
El siguiente paso consiste en identificar cada uno de los componentes de la garra (Figura 18). En color rojo y azul están representadas las aletas donde esta diferencia de colores indica la alternancia en su disposición para evitar colisiones durante la activación. Asimismo, el movimiento de arrastre del deslizador representado en color naranja, permite controlar la rotación de las aletas a través de los brazos que conectan estos dos elementos. Este deslizador está conectado a través de las aperturas del cilindro de color cian a una varilla roscada ubicada en el interior del cilindro y la cual está acoplada a un motor paso a paso (también alojado dentro de este cilindro) que permite controlar la apertura y cierre de la garra.
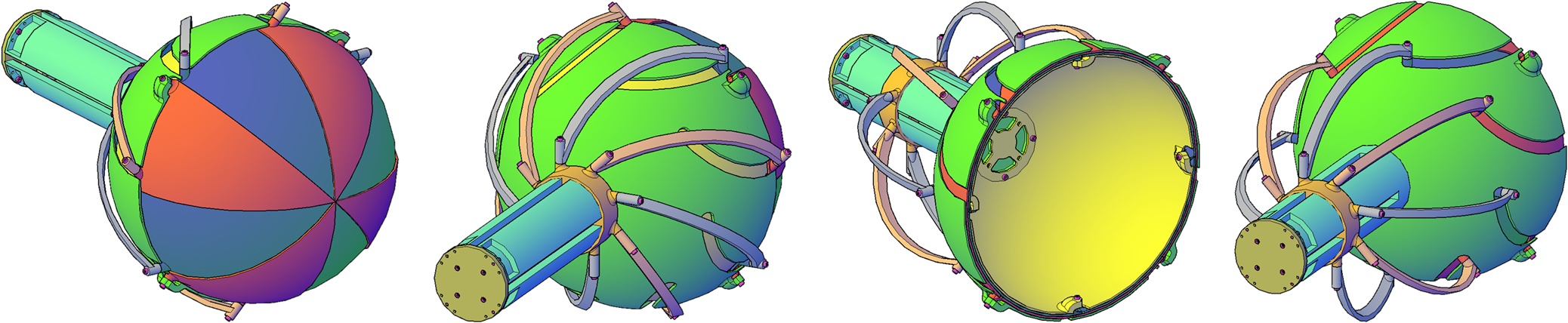
Figura 18: Perspectivas tridimensionales de la garra desarrollada en posición abierta y cerradas con identificación de los componentes.
Por último, el material, pesos y cantidad de cada una de las partes están representados en la siguiente tabla teniendo un peso total de 2.26 kilos (Tabla 4).
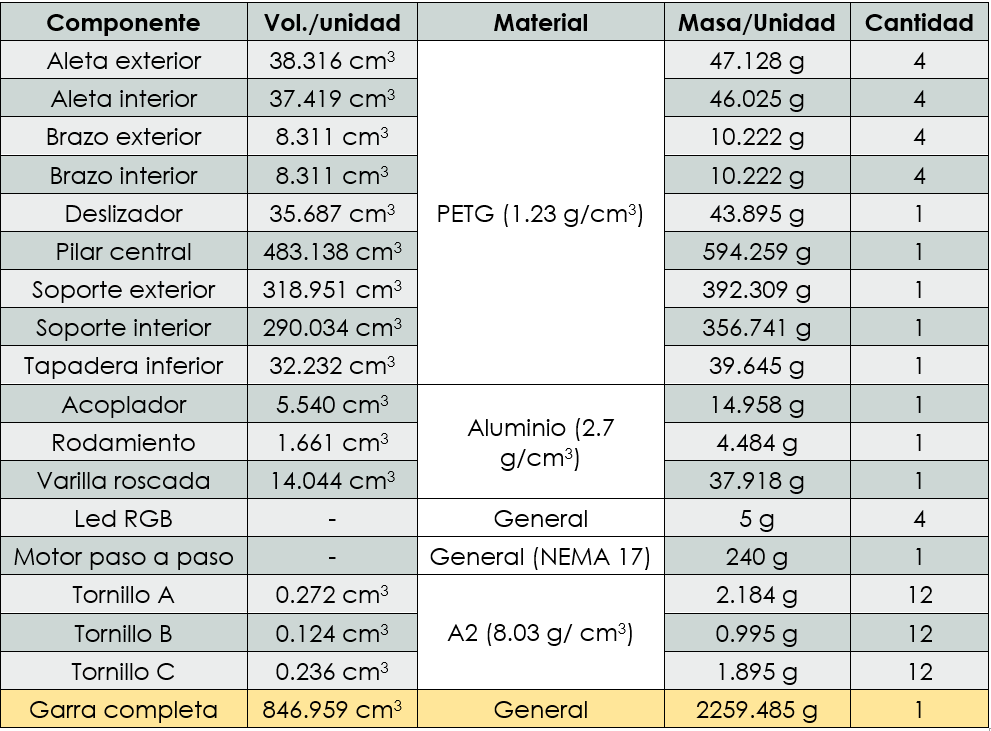
Tabla 4: Información de las masas de cada componente de la garra.
3.3. Análisis
Tras definir el diseño del dispositivo, se procede a efectuar el respectivo análisis de posición, velocidad y aceleración. Sin embargo, antes de comenzar con su desarrollo es muy importante definir cuáles serán las variables de entrada, las variables de control y las variables de salida (Figura 19).
- Las variables de entrada serán aquellas variables por defecto en el problema y que el diseñador no puede controlar. En nuestro caso, las longitudes de los eslabones “a”, “b” y “c”.
- Las variables de control serán aquellas variables que el diseñador puede manipular para provocar cambios en las variables de salida. En nuestro caso, la longitud del eslabón “d”.
- Las variables de salida serán aquellas variables cuyo valor dependa de las variables de control. En nuestro caso, la posición, velocidad y aceleración del punto A.
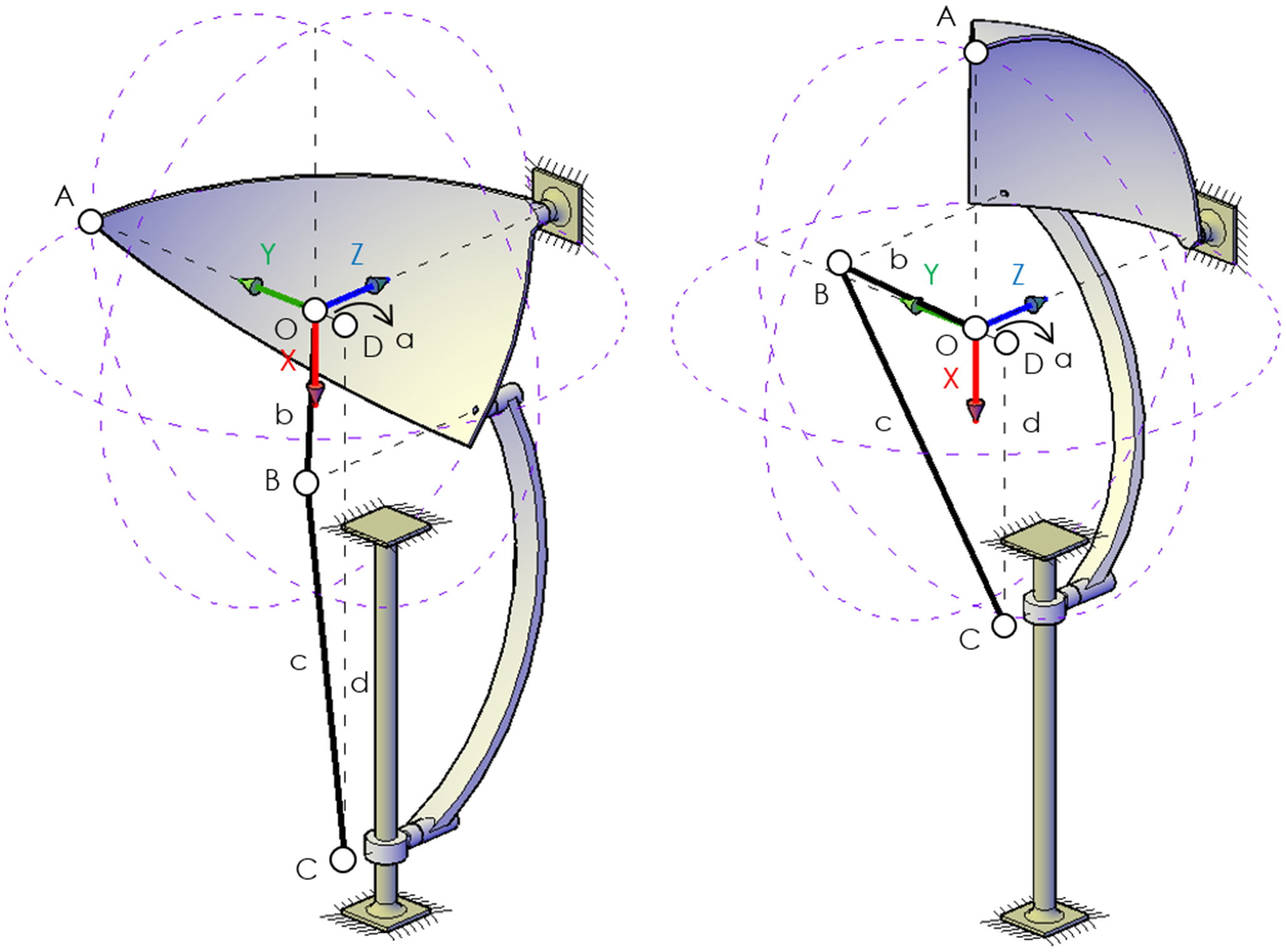
Figura 19: Identificación de las variables que intervienen en el problema.
3.3.1. Análisis de posición
El primer análisis que se efectúa es el de posición. Dado que el desarrollo matemático de las respectivas ecuaciones puede resultar algo tedioso, se ha omitido dicha parte en esta publicación y se deja a elección del lector su consulta en el documento del proyecto. Una vez que las ecuaciones que rigen el comportamiento de posición han sido obtenidas, se ha representado en la siguiente figura (Figura 20) las curvas que predicen la evolución de la ubicación del punto A. Estas curvas están en función del ángulo de giro de la aleta con respecto a la variable de control definida por la longitud del eslabón “d” y para diferentes valores de la longitud del eslabón “b”.
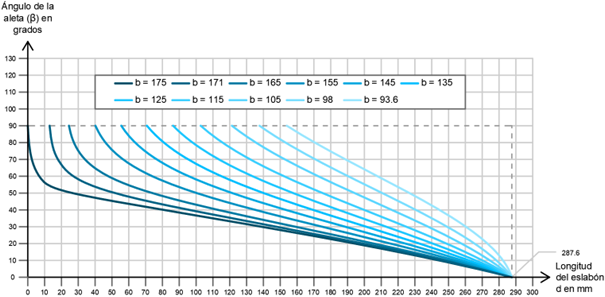
Figura 20: Evolución del ángulo de cierre de la garra ( ) frente al valor de la corredera (eslabón d) para diferentes valores de la manivela (eslabón b) (unidades en grados y en mm).
) frente al valor de la corredera (eslabón d) para diferentes valores de la manivela (eslabón b) (unidades en grados y en mm).
3.3.2. Análisis de velocidad
Con respecto al análisis de velocidad, el proceso de obtención de las ecuaciones es muy similar al análisis de posición: obtención de las ecuaciones de lazo vectorial, derivar estas ecuaciones con respecto al tiempo, determinación de las velocidades angulares y despeje de las velocidades lineales de los eslabones “b” y “c”. Finalmente, la velocidad lineal del punto A se determina aplicando la ecuación de la cinemática relativa en velocidad para un sólido rígido.
En la gráfica de las siguiente figura (Figura 21) se ha representado el valor de le velocidad lineal del punto A para diferentes valores de la variable de entrada y para diferentes situaciones de longitud en el eslabón “b”. De esta gráfica se puede deducir que a medida que le valor de la longitud del eslabón “b” aumenta, la velocidad del punto A tiende a ser constante durante un mayor intervalo de la variable de entrada.
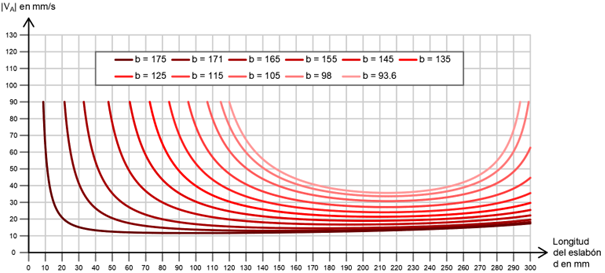
Figura 21: Evolución de la velocidad del vértice de las aletas frente al valor de la corredera (eslabón d) para diferentes valores de la manivela (eslabón b) (unidades en mm/s y en mm).
3.3.3. Análisis de aceleración
Por último, el análisis de aceleración requiere de un desarrollo matemático análogo al análisis de velocidad y aplicando en último lugar la ecuación de la cinemática relativa en aceleración para un sólido rígido. Como aspecto a resaltar, en la gráfica adjunta (Figura 22) se puede observar como a medida que la longitud del eslabón “b” aumenta, los tramos con una aceleración constante también crecen.
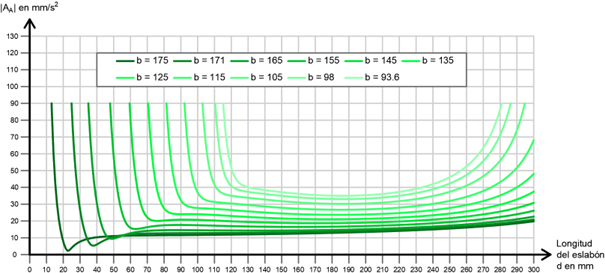
Figura 22: Evolución de la aceleración del vértice de las aletas frente al valor de la corredera (eslabón d) para diferentes valores de la manivela (eslabón b) (unidades en mm/s2 y en mm).
3.4. Circuito electrónico
En lo que se refiere al circuito electrónico para controlar el funcionamiento de la garra robótica, se ha optado por el uso de un microcontrolador Atmega8A debido a que por defecto tiene 3 señales PWM las cuales serán muy útiles para controlar la iluminación de los leds RGB de la garra. Asimismo y como se puede apreciar en la siguiente figura (Figura 23), este microcontrolador posee un total de 11 salidas o entradas digitales y 6 entradas analógicas lo cual lo convierten en un dispositivo bastante versátil.
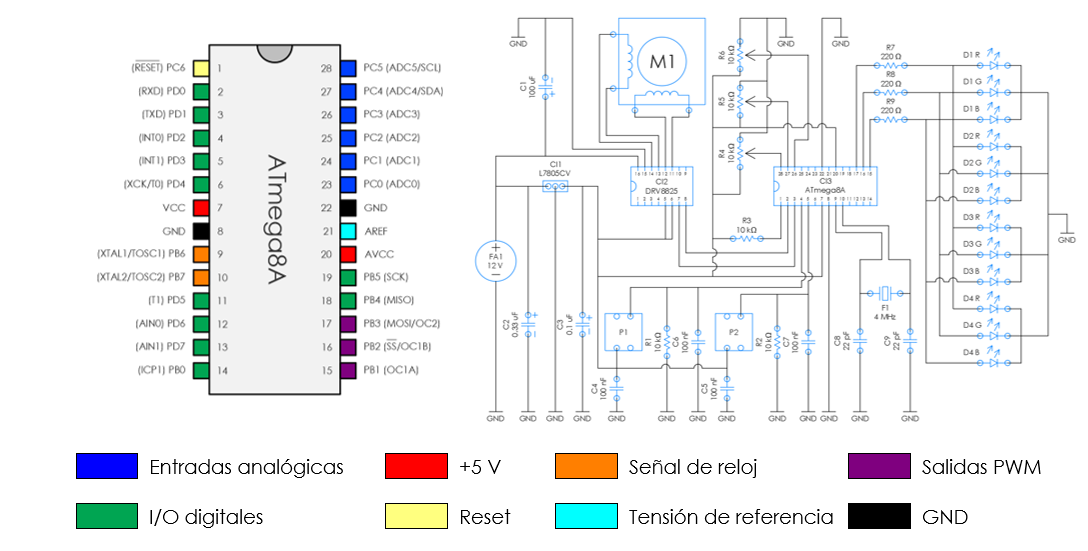
Figura 23: Microcontrolador seleccionado y esquema del circuito electrónico completo.
3.5. Presupuesto
La última sección del desarrollo y análisis de la garra robótica se corresponde con el presupuesto del dispositivo. Como es lógico, la mayor partida presupuestaria concentra en el hardware estructural de la garra robótica seguido del coste de las partes comercialmente disponibles y del coste de la electrónica. De esa manera, la suma de todos esos importes asciende a un precio total aproximado de 95 euros (Tabla 5).
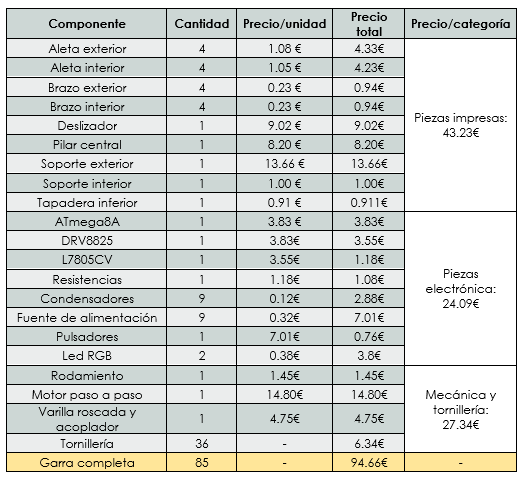
Tabla 5: Información de los precios de cada componente de la garra.
4. Conclusiones
4.1. Integración de la garra en un brazo robótico
Una vez terminado el estudio de la garra desarrollada, el siguiente paso es implementarla en un brazo robótico (modelo IRB2600 de ABB) (Figura 24). Asimismo, es importante destacar que la interfaz de la garra robótica en la base inferior del cilindro se ha diseñado acorde con la interfaz de conexión de este brazo robótico. Por último, también se ha comprobado que este brazo robótico sea capaz de operar con una garra de peso igual o superior al modelo diseñado de 2.26 kilos.
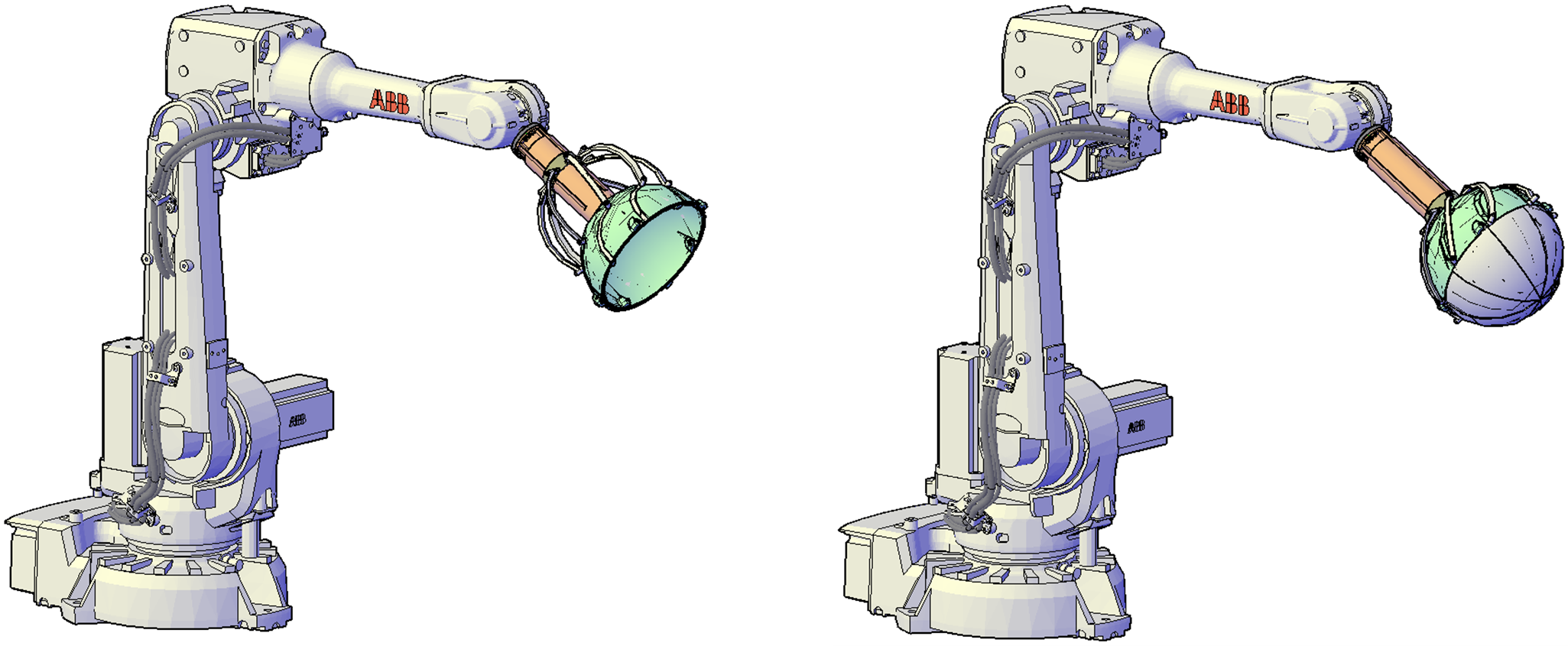
Figura 24: Integración de la garra robótica en un brazo robótico IRB 2600.
4.2. Campos de aplicaciones
Dentro de los múltiples campos de aplicación donde este dispositivo podría tener éxito, se ha encontrado un nicho tanto en la captura y transporte de chatarra en forma de pequeños fragmentos como en el agarre y manipulación de alimentos en forma granular (Figura 25). En el caso en el que fuera necesario la manipulación de volúmenes de mayor tamaño al espacio interior que puede albergar la garra, sería imprescindible la eliminación de algunas de las aletas para permitir que los objetos agarrados sobresalgan por las aberturas que se obtienen al eliminar dichas aletas (las garras en el mercado utilizan una estrategia de diseño similar).

Figura 25: (izquierda y centro) Garras robóticas para la captura de chatarra – Acemex Electroamerica ; (derecha) Procesado de alimentos en forma granular - Greencan.
4.3. Epílogo
El Proyecto Fin de Master desarrollado ha permitido el diseño y análisis de un dispositivo el cual funciona correctamente a nivel mecánico sin ningún tipo de colisión ni puntos de incertidumbre geométrica durante su accionamiento. Esto se deduce del análisis de posición en donde las curvas de evolución no plantean la existencia de particiones en su recorrido y, por lo tanto, de dobles soluciones.
Su control se ha llevado a cabo mediante un circuito electrónico donde se ha dado preferencia al uso de un motor paso a paso y de un driver en lugar de un servomotor y un puente en H debido a la facilidad de obtener estos componentes comercialmente.
Por último, el software programado (se ruega al lector que se remita al documento del proyecto para su consulta) permite considerar y corregir situaciones incompatibles con el correcto funcionamiento de la garra como es la activación simultanea de ambos pulsadores de giro o la sobreexposición del motor a un giro permanente evitando un sobrecalentamiento del mismo.
Referencias
Akgün, Y., Gantes, C. J., Kalochairetis, K. E., & Kiper, G. (2010). A novel concept of convertible roofs with high transformability consisting of planar scissor-hinge structures. Engineering Structures, 32(9), 2873–2883. https://doi.org/10.1016/j.engstruct.2010.05.006
Alegria Mira, L., Thrall, A. P., & De Temmerman, N. (2014). Deployable scissor arch for transitional shelters. Automation in construction, 43, 123–131. https://doi.org/10.1016/j.autcon.2014.03.014
Arnouts, L. I. W., Massart, T. J., De Temmerman, N., & Berke, P. Z. (2018). Computational modelling of the transformation of bistable scissor structures with geometrical imperfections. Engineering Structures, 177, 409–420. https://doi.org/10.1016/j.engstruct.2018.08.108
Arnouts, L. I. W., Massart, T. J., De Temmerman, N., & Berke, P. Z. (2020). Multi-objective optimisation of deployable bistable scissor structures. Automation in Construction, 114(103154), 103154. https://doi.org/10.1016/j.autcon.2020.103154
Babaee, S., Pajovic, S., Rafsanjani, A., Shi, Y., Bertoldi, K., & Traverso, G. (2020). Bioinspired kirigami metasurfaces as assistive shoe grips. Nature Biomedical Engineering, 4(8), 778–786. https://doi.org/10.1038/s41551-020-0564-3
Cai, J., Deng, X., Feng, J., & Xu, Y. (2014). Mobility analysis of generalized angulated scissor-like elements with the reciprocal screw theory. Mechanism and Machine Theory, 82, 256–265. https://doi.org/10.1016/j.mechmachtheory.2014.07.011
Chen, Y., & Feng, J. (2012). Folding of a type of deployable origami structures. International Journal of Structural Stability and Dynamics, 12(06), 1250054. https://doi.org/10.1142/s021945541250054x
Chen, Y., You, Z., & Tarnai, T. (2005). Threefold-symmetric Bricard linkages for deployable structures. International Journal of Solids and Structures, 42(8), 2287–2301. https://doi.org/10.1016/j.ijsolstr.2004.09.014
Christoforou, E. G., Müller, A., Phocas, M. C., Matheou, M., & Arnos, S. (2015). Design and control concept for reconfigurable architecture. Journal of Mechanical Design (New York, N.Y.: 1990), 137(4), 042302. https://doi.org/10.1115/1.4029617
Escrig, F., & Valcarcel, J. P. (1993). Geometry of expandable space structures. International Journal of Space Structures, 8(1–2), 71–84. https://doi.org/10.1177/0266351193008001-208
Escrig, F., Sanchez, J., & Valcarcel, J. P. (1996). Two way deployable spherical grids. International Journal of Space Structures, 11(1–2), 257–274. https://doi.org/10.1177/026635119601-231
Fomin, A., Dvornikov, L., & Paik, J. (2017). Calculation of general number of imposed constraints of kinematic chains. Procedia Engineering, 206, 1309–1315. https://doi.org/10.1016/j.proeng.2017.10.636
Fomin, A., Dvornikov, L., Paramonov, M., & Jahr, A. (2015) To the theory of mechanisms subfamilies. International Conference on Mechanical Engineering, Automation and Control Systems (MEACS2015), 124, 1–7. https://doi.org/10.1088/1757-899X/124/1/012055
Gantes, C. J., Connor, J. J., Logcher, R. D., & Rosenfeld, Y. (1989). Structural analysis and design of deployable structures. Computers & Structures, 32(3–4), 661–669. https://doi.org/10.1016/0045-7949(89)90354-4
Gantes, C., Connor, J. J., & Logcher, R. D. (1991). Combining numerical analysis and engineering judgment to design deployable structures. Computers & Structures, 40(2), 431–440. https://doi.org/10.1016/0045-7949(91)90368-v
García-Mora, C. J., & Sánchez-Sánchez, J. (2020). Geometric method to design bistable and non - bistable deployable structures of straight scissors based on the convergence surface. Mechanism and Machine Theory, 146(103720), 103720. https://doi.org/10.1016/j.mechmachtheory.2019.103720
García-Mora, C. J., & Sánchez-Sánchez, J. (2021). The convergence surface method for the design of deployable scissor structures. Automation in Construction, 122(103488), 103488. https://doi.org/10.1016/j.autcon.2020.103488
Jin, L., Forte, A. E., Deng, B., Rafsanjani, A., & Bertoldi, K. (2020). Kirigami-inspired inflatables with programmable shapes. Advanced Materials (Deerfield Beach, Fla.), 32(33), e2001863. https://doi.org/10.1002/adma.202001863
Kirsch, U. (1982). Synthesis of structural geometry using approximation concepts. Computers & Structures, 15(3), 305–314. https://doi.org/10.1016/0045-7949(82)90021-9
Liu, S., Lv, W., Chen, Y., & Lu, G. (2016). Deployable prismatic structures with rigid origami patterns. Journal of Mechanisms and Robotics, 8(3), 031002. https://doi.org/10.1115/1.4031953
Overvelde, J. T. B., Weaver, J. C., Hoberman, C., & Bertoldi, K. (2017). Rational design of reconfigurable prismatic architected materials. Nature, 541(7637), 347–352. https://doi.org/10.1038/nature20824
Pérez-Almagro, M. C. (2017). El archivo fotográfico del arquitecto Emilio Pérez Piñero. Estructura y análisis documental. Anales de documentación, 20(2). https://doi.org/10.6018/analesdoc.20.2.277831
Teoh, Z. E., Phillips, B. T., Becker, K. P., Whittredge, G., Weaver, J. C., Hoberman, C., Gruber, D. F., & Wood, R. J. (2018). Rotary-actuated folding polyhedrons for midwater investigation of delicate marine organisms. Science Robotics, 3(20), eaat5276. https://doi.org/10.1126/scirobotics.aat5276
Truby, R., Katzschmann, R., Lewis, J., Rus, D. (2019) Soft Robotic Fingers with Embedded Ionogel Sensors and Discrete Actuation Modes for Somatosensitive Manipulation. IEEE Conference Publication | IEEE Xplore. https://ieeexplore.ieee.org/document/8722722
Los más leídos
ADRIÀ NOLLA DEL VALLE, (2023)
La Cartera Adaptada: adaptando la cartera permanente a los ciclos económicos Leer InvestigaciónAlberto Conchillo Guantes, (2023)
Impacto del impuesto de sociedades en el comportamiento de las empresas Leer InvestigaciónFrancisco Javier Roldán de la Rosa, (2023)
Historia y evolución de la Farmacovigilancia Leer Investigación


